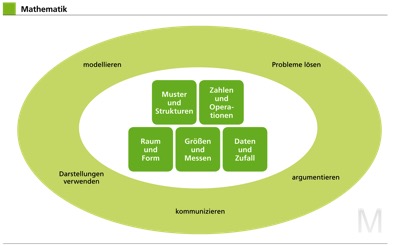
The competence structure model of mathematics is based on the educational standards in mathematics for the primary level. It is divided into two areas, which are always linked together in the classroom: in the process-related competences (outer ring) and in the five subject areas (inner fields) that reflect the subject-specific content. In this way, students always acquire process-related and content-related skills in close contact with one another.
Model modellieren
When modeling students take factual texts or other representations of the reality of life relevant information and translate these into the language of mathematics. They recognize mathematical connections and use them to arrive at a solution, which they finally apply to the concrete situation. Primary school is based on mathematical approaches and modeling skills. Your acquisition is fundamental to solving application-related mathematical problems and has a lasting and consistent impact on all other learning areas in the subject curriculum. That is why starting points for modeling processes are always offered throughout the primary school mathematics lessons.
Solve problems Probleme lösen
Students learn to solve problems by applying their existing mathematical knowledge, skills and abilities in dealing with challenging or unknown tasks, developing and using solution strategies. In doing so, they must also be able to process relevant information from various sources in a targeted manner and present solutions plausibly.
Communicate Kommunizieren
Communicating skills are also used by primary school children in mathematics in cooperative and interactive teaching processes. They use mathematical technical terms and signs correctly and gradually gain experience in working on math problems together as well as in describing their solutions in a comprehensible way.
Argue Argumentieren
The learners are becoming increasingly confident in their argumentation by questioning mathematical statements and checking for correctness or plausibility (eg in the case of salmon situations: can this be correct?). In doing so, they recognize mathematical relationships, develop solutions within the scope of their possibilities, and look for reasons appropriate to the situation, which they explain on their own or together with others. Unusual calculation methods also make you think and challenge you to argue.
Use Representations Darstellungen verwenden
The students acquire and consolidate this competence by also reading and developing suitable sketches, calculations or simple tables for mathematical problems, choosing between different representations and using them. In elementary school, the children learn to transfer one presentation into another (eg a table in a diagram or concrete action situations in a sketch) as well as to compare and evaluate different representations.
GRADES PROFILES
The students use basic ideas about the structure of the decimal system as well as arithmetic operations. In doing so, they solve tasks for the four basic arithmetic operations in the number range to hundreds, both with the help of notes and in the head. One-to-twenty tasks and one-off tasks with 1, 2, 5, 10 as well as squares sets of the small multiplication tables are used automatically and flexibly.
In exchange with others, the students compare their solutions and check the results both mathematically and out of context.They solve simple combinatorial tasks. Students recognize and describe patterns and structures. They use regularities and strategies in arithmetic and orient themselves in their immediate environment; Spatial relationships between objects of everyday life (eg left / right), describe both in terms of their own perspective and that of another person. Students learn to describe properties of geometric surface and body shapes, while studying the surface contents and the sizes of simple planar figures and compare them. Lower Elementary pupils produce geometric patterns and describe their regularities.
The students acquire ideas about the size ranges monetary value (ct and €), time periods (min and h) and lengths (cm and m) and apply them to solving simple problems from their world of experience. Simple problems in everyday situations (e.g. shopping or purchasing situations) solve the students with mathematical means. For this they extract information, for example, from actions, pictorial representations, simple texts, formulate questions and tasks, and apply solutions.
The students collect data on problems from their world of experience, using appropriate representations (e.g. tally lists, tables, simple graphs) and describe both their approaches and the information content of the resulting representations.Students develop simple random experiments and first problem-solving strategies (e.g. systematic sampling) and use basic terms of probability to describe the random experiments.